1522. Optimal
Binary Search Tree
Given
a set S = {e1, e2, …, en} of n
distinct elements such that e1
< e2 < … < en and considering a binary
search tree of the elements of S, it is desired that higher the query frequency
of an element, closer will it be to the root.
The
cost of accessing an element ei of S in a tree cost(ei) is equal to the
number of edges in the path that connects the root with the node that contains
the element. Given the query frequencies of the elements of S, (f(e1),
f(e2), ..., f(en)), we say that the
total cost of a tree is the following summation:
f(e1) * cost(e1)
+ f(e2) * cost(e2) + … + f(en)
* cost(en)
In this manner, the tree
with the lowest total cost is the one with the best representation for
searching elements of S. Because of this, it is called the Optimal Binary
Search Tree.
Input. Contains
several instances, one per line. Each line will start with a number n (1 ≤ n ≤ 250), indicating the size of S. Following n, in the same line, there will be n non-negative integers representing the
query frequencies of the elements of S: f(e1),
f(e2), ..., f(en) (0 ≤ f(ei) ≤ 100).
Output.
For each instance of the input, you must print a line in the output with the
total cost of the Optimal Binary Search Tree.
|
Sample
input |
Sample
output |
|
1 5 3 3 1 7 7 4 10 6 2 3
5 7 6 1 3 5 10 20 30 |
0 5 49 63 |
SOLUTION
dynamic programming
Algorithm analysis
Imagine that you
have written a translation program and posted it on the Internet. Words are
located at the vertices of a binary tree.
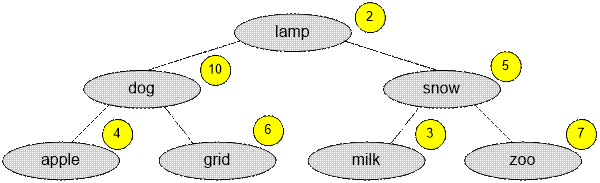
After a while,
for each word ei (key), you learned the number of requests f(ei) to it. The values f(ei) are marked in yellow. The cost of the current Search Tree is
10 + 4 * 2 + 6 * 2 + 5 + 3 * 2 + 7 * 2 = 55
The question
arises: is it possible to change the structure of the tree so that to minimize the
indicated cost?
For this
example, the Optimal Binary Search Tree has the form:
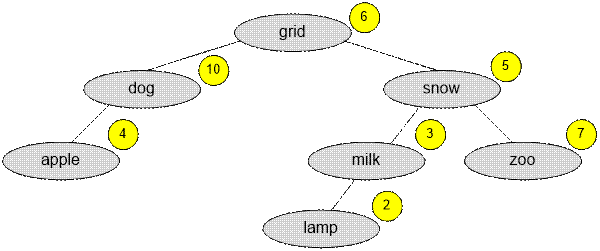
Its cost is
10 + 4 * 2 + 5 +
3 * 2 + 7 * 2 + 2 * 3 = 49
Let Ti,j be the cost of an
optimal binary search tree that can be constructed from the elements ei, ei+1, …, ej. Obviously, Ti,i = 0 (the cost of a search tree from one
vertex is equal to zero). For i < j, the recurrence
takes place:
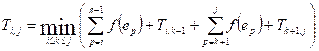
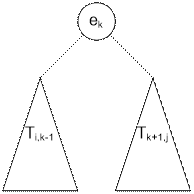
Put the element ek at the root. The cost to build the left subtree is Ti,k-1.
The
cost to build the right subtree is Tk+1,j. Moreover,
since the root of the left subtree is one level below ek, to take into
account the cost of the left subtree, it is necessary to add the sum of the
frequencies of all its elements, that is, the value 
. Likewise, when calculating the value of the right subtree,
add 
.
For i > j set
Ti,j = 0.
Note also that
the solution of the problem optimal
binary search tree is similar to solution of the problem optimal matrices multiplication.
Example
Consider a set S, with three elements e1 < e2 < e3 with frequencies 3, 1 and 7. The frequencies of the
elements can follow in any order. Possible search trees are:
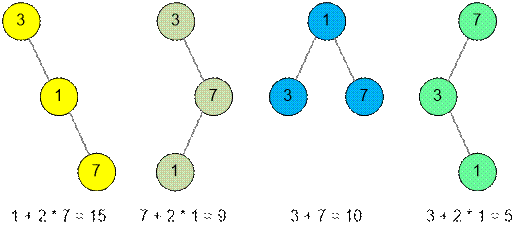
cost of the trees
The figures do not show all possible trees, but note that
the rightmost tree is optimal, its cost is the smallest among all possible ones
and equals to 5.
Consider the
fourth test. The optimal binary search tree has the form:
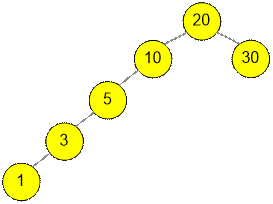
Then
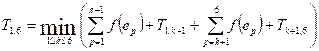
The cost of the
left subtree (if 10 is the root):
T1,4
= 5 + 3 * 2 + 1 * 3 = 14
The cost of the right subtree (if 30 is the root): T6,6
= 0.
If the required minimum is
attained for k = 5, then
= (1 + 3 + 5 + 10) +
14 + (30) + 0 = 63,
which equals to the cost of
the entire tree.
Algorithm realization
Declare the constants.
#define MAX 300
#define
INF 0x3F3F3F3F
Declare the arrays.
int m[MAX], sum[MAX];
int t[MAX][MAX];
Store the input
frequencies of the elements in the array m, the array sum will store the
partial sums of the frequencies: sum[i] = 
. The values Ti,j will be stored in array t.
Partial
sum 
is
returned by the function weight(i, j).
int weight(int
i, int j)
{
if (i > j)
return 0;
return sum[j]
- sum[i-1];
}
Function go(i, j) returns the
value of Ti,j.
int go(int
i, int j)
{
if (i > j)
return 0;
if (t[i][j]
== INF)
{
for (int k = i; k <= j; k++)
{
int temp = go(i,k-1) + go(k+1,j) + weight(i,k-1) +
weight(k+1,j);
if (temp
< t[i][j]) t[i][j] = temp;
}
}
return
t[i][j];
}
The main part of
the program. Read the
frequencies of elements, set t[i][i] = Ti,i = 0. The rest of the
values of array t are set to infinity.
while(scanf("%d",&n)
== 1)
{
memset(t,0x3F,sizeof(t));
for(i = 1; i
<= n; i++)
{
scanf("%d",&m[i]);
t[i][i] = 0;
}
Compute the partial sums of array m.
sum[0] = 0
for(i = 1; i
<= n; i++)
sum[i] = sum[i-1] + m[i];
Compute the value of T1,n making the call go(1, n). Print the answer.
go(1,n);
printf("%d\n",t[1][n]);
}
Java realization
import java.util.*;
public class Main
{
static int t[][],
sum[];
static int
weight(int i, int j)
{
if (i >
j) return 0;
return sum[j] - sum[i-1];
}
static int go(int i, int j)
{
int k, temp;
if (i >
j) return 0;
if (t[i][j] == Integer.MAX_VALUE)
{
for (k = i; k
<= j; k++)
{
temp = go(i,k-1) +
go(k+1,j) + weight(i,k-1) +
weight(k+1,j);
if (temp <
t[i][j]) t[i][j] = temp;
}
}
return t[i][j];
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
while(con.hasNextInt())
{
int n = con.nextInt();
t = new int[n+1][n+1];
for(int i = 1;
i <= n; i++)
Arrays.fill(t[i], Integer.MAX_VALUE);
int m[] = new int[n+1];
sum = new int[n+1];
for(int i = 1;
i <= n; i++)
{
m[i] = con.nextInt();
t[i][i] =
0;
}
sum[0] =
0;
for(int i = 1;
i <= n; i++)
sum[i] = sum[i-1] +
m[i];
go(1,n);
System.out.println(t[1][n]);
}
con.close();
}
}